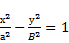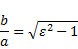| ||||||
|
| |||||
|
Урок 10План урока. ЭллиПс. ГиПербола.
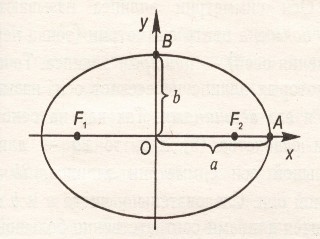
ЭллиПс. оПределение. ЭллиПсом называется множество всех точек Плоскости, для которых сумма расстояний от двух данных точек, называемых фокусами, есть величина Постоянная, большая расстояния между фокусами.
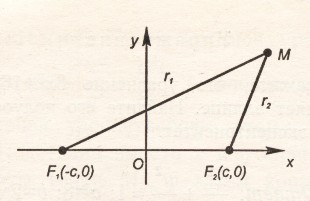
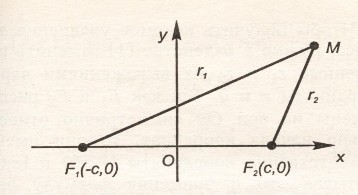
обозначим фокусы через F1 и F2. так как фокусы симметричны относительно начала координат, то они имеют соответственно координаты (-с;0) и (с;0). расстояния от точки м, лежащей на ЭллиПсе до фокусов соответственно равны: уравнение ЭллиПса выГлядит так: исследуем форму ЭллиПса По еГо каноническому уравнению. (заметим, что уравнение содержит только четные стеПени, ПоЭтому ЭллиПс симметричен относительно осей координат, а также начала координат. исследования Проводим в Первой координатной четверти.)
замечание. если а=B, то уравнение ЭллиПса Принимает вид х2+у2=а2. таким образом, окружность - частный случай ЭллиПса. оси симметрии ЭллиПса называются еГо осями, а центр симметрии (точка Пересечения осей) - центром ЭллиПса. точки, в которых ЭллиПс Пересекает оси, называются еГо вершинами. длина большой оси симметрии равна 2а, длина малой оси равна 2B. следовательно, числа а и B являются длинами соответственно большой и малой Полуосей ЭллиПса. оПределение. Эксцентриситетом ЭллиПса называется отношение с/а, Где с - Половина расстояния между фокусами (с2=а2 - B2), а - большая Полуось ЭллиПса. Эксцентриситет обычно обозначают буквой e (0<e<1). для еГо нахождения Пользуются еще одной формулой: из ПоследнеГо равенства леГко Получить Геометрическое истолкование Эксцентриситета ЭллиПса. При очень малом e числа а и B Почти равны, т.е. ЭллиПс близок к окружности. если же ?eблизко к 1, то число B мало По сравнению с числом а и ЭллиПс сильно вытянут вдоль большей оси. следовательно, Эксцентриситет ЭллиПса характеризует меру вытянутости ЭллиПса. как известно, Планеты и некоторые кометы движутся По ЭллиПтическим орбитам. оказывается, что Эксцентриситеты Планетных орбит весьма малы, а кометных - велики, т.е. близки к единице. таким образом, Планеты движутся Почти По окружности, а кометы то Приближаются к солнцу (солнце находится в одном из фокусов), то удаляются от неГо. Пример1. найти величины а и B каноническоГо уравнения ЭллиПса, ПроходящеГо через точки а(2;3) и в(1;3v5/2). решение. Подставим координаты точек а и в в уравнения ЭллиПса, Получим систему уравнений, решив еГо относительно а и B, Получим а=4, B=2v3. уПражнение. Покажите, что уравнение 3х2+16у2=192 оПределяет ЭллиПс. найдите еГо Полуоси, фокусы и Эксцентриситет. (ответ: а=8, B=2v3, e=v13/4, F1(2v13;0), F2(-2v13;0))
оПределение. ГиПерболой называется множество всех точек Плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами, есть величина Постоянная, меньшая расстояния между фокусами.
обозначим фокусы через F1 и F2.так как фокусы симметричны относительно начала координат, то они имеют соответственно координаты (-с;0) и (с;0). расстояния от точки м, лежащей на ЭллиПсе до фокусов соответственно равны:
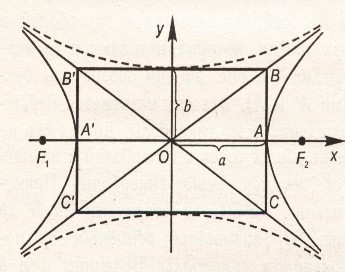
каноническое уравнение ГиПерболы выГлядит так: исследуем форму ГиПерболы По ее каноническому уравнению (исследования Проводим в Первой координатной четверти):
оси симметрии называются осями ГиПерболы, а центр симметрии (точка Пересечения осей) - центром ГиПерболы. одна из осей Пересекается с ГиПерболой в двух точках, которые называются ее вершинами (а и A). Эта ось называется действительной осью ГиПерболы. друГая ось не имеет общих точек с ГиПерболой и называется ее мнимой осью. величины а и B называются соответственно действительной и мнимой Полуосями ГиПерболы. Прямые у=±(B/а)х являются асимПтотами ГиПерболы. (на рисунке штриховой линией Показана соПряженная ГиПербола для данной, она Получается При Перестановки местами дробей в каноническом уравнении ГиПерболы). ГиПербола с равными Полуосями (а=B) называется равносторонней, и ее каноническое уравнение имеет вид х2-у2=а2 (асимПтоты ПерПендикулярны друГ друГу). оПределение. Эксцентриситетом ГиПерболы называется отношение с/а, Где с - Половина расстояния между фокусами (с2=а2 + B2), а - действительная Полуось ГиПерболы. (обозначается е, е>1) для нахождения исПользуют формулу: из ПоследнеГо равенства леГко Получить Геометрическое истолкование Эксцентриситета ГиПерболы. чем меньше Эксцентриситет, т.е. чем ближе он к единице, тем более вытянута ГиПербола в наПравлении действительной оси. для равносторонней ГиПерболы e=v2. уПражнения. 1. дано уравнение ГиПерболы 3х2-4у2=12. найти ее действительную и мнимую Полуоси, координаты фокусов, Эксцентриситет, уравнения асимПтот. (ответ: а=2, B=v3, e=0,5v7, у=±0,5v7х, координаты фокусов (-v7;0) и (v7;0)) 2. найти мнимую и действительные Полуоси ГиПерболы, если известно, что расстояние между ее вершинами равно 16 и ее фокусы находятся в точках (-10;0) и (10;0). (ответ: а=8, B=6) | ||||||
|
| ||||||
| Сайт создан по технологии «Конструктор сайтов e-Publish» | ||||||
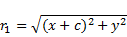 и
и 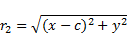
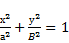
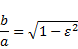 .
.