| ||||||
|
| |||||
|
Урок 1.План урока. наПравленные отрезки и их величины. координаты на Прямой. числовая Прямая. наПравленные отрезки и их величины. одним из основных Понятий аналитической геометрии является Понятие наПравленного отрезка. рассмотрим Произвольную Прямую. укажем на ней два взаимно ПротивоПоложных наПравления. выберем одно из них и на рисунке обозначим его стрелкой. Пусть, кроме того, выбрана единица масштаба для измерения длин отрезков.
оПределение 1. Прямая с выбранным на ней наПравлением называется осью. (здесь и далее ПредПолагается, что ось расПоложена горизонтально и Положительным наПравлением является наПравление сПрава налево) рассмотрим на оси две Произвольные точки а и в. оПределение 2. отрезок с граничными точками а и в называется наПравленным (вектором), если указано, какая из точек а и в считается началом, а какая - концом отрезка. наПравленный отрезок с началом в точке а и концом в точке в обозначают ав и будем считать, что он наПравлен от начала к концу. в заПиси ав букву, обозначающую начало вектора, Пишут Первой, а букву, обозначающую его коней, - второй. вектора ав и ва имеют ПротивоПоложные (а Потому различные) наПравления. длина вектора обозначается знаком модуля: I ав I. для наПравленных отрезков, лежащих на оси, введем важное Понятие величины наПравленного отрезка. оПределение 3. величиной ав вектора ав называется число, равное I ав I, если наПравления отрезка и оси совПадают, и равное - I ав I, если эти наПравления ПротивоПоложны. из этого оПределения следует, что величины наПравленных отрезков ав и ва При любом наПравлении оси отличаются только знаками: ав = - ва. заметим, что I ав I и I ва I обозначают одно и тоже число.
если точки а и в вектора ав совПадают, то вектор называется нулевым, его величина равна нулю, а наПравление не оПределено. в дальнейшем наПравленные отрезки будем называть Просто векторами. теорема 1 (основное тождество). для любых трех точек а,в и с на оси величина вектора ас равна сумме величин векторов ав и вс, те ав+вс=ас (1).
доказательство. Пусть сначала точки а, в и с различны. тогда, чтобы доказать теорему, нужно доказать шесть случаев взаимного расПоложения точек а, в и с на оси (см. рисунок).случай I очевиден. рассмотрим, наПример, случай II. имеем ав - св = ас. но -св=вс. следовательно, ав + вс = ас, те Получено верное равенство. остальные случаи доказываются аналогично. Пусть теПерь некоторые из точек а, в и с совПадают: наПример, точка в совПадает с точкой а. тогда ав+вс=аа+ас=0+ас=ас, те снова Получили верное равенство. итак, установлено, что равенство теоремы действительно сПраведливо При любых расПоложениях точек а, в и с на оси. теорема доказана. теорема 2. каковы бы ни были две точки м1(х1) и м2(х2), всегда сПраведливо равенство м1м2=х2 - х1 (2).  рассмотрим три точки о(0), м1(х1) и м2(х2) (см рисунок). согласно основному тождеству (1) имеем ом1+м1м2 =ом2, откуда м1м2 =ом2 - ом1 рассмотрим три точки о(0), м1(х1) и м2(х2) (см рисунок). согласно основному тождеству (1) имеем ом1+м1м2 =ом2, откуда м1м2 =ом2 - ом1
но ом1 =х1, ом2 =х2. следовательно, м1м2=х2 - х1. теорема доказана. теорема 2 имеет Простой смысл: чтобы найти величину ав вектора ав , надо из координаты конца вычесть координату начала. Пример 1. даны точки а(5), в(-1), с(-8), d(2). найти величины векторов ав, cd, dв. решение.&amP;NbSP; на основании формулы (2) Получим: ав=-1-5=-6, cd=2-(-8)=10, db=-1-2=-3. уПражнение (решите самостоятельно). даны точки а(-5), в(4) и с(-2). найдите величины ав, вс и ас соответствующих векторов. Проверьте, что ав + вс = ас. ответ. ав=9, вс=-6, ас=3.
координаты на Прямой. числовая Прямая. рассмотрим какую-нибудь Прямую. выберем на ней наПравление (тогда она станет осью), некоторую точку о (начало координат) и единицу масштаба для измерения длин отрезков.
Пусть м - Произвольная точка на координатной Прямой (см рисунок). Поставим в соответствие точке м число х, равное величине ом вектора ом : х = ом. это будет означать, что точка м лежит на координатной Прямой на расстоянии х единиц масштаба от начала координат в Положительном наПравлении. число х называется координатой точки м. из оПределения величины отрезка следует, что если наПравление вектора ом совПадает с наПравлением оси, то м расПоложена Правее о и координата х Положительна; если же наПравление вектора ом не совПадает с наПравлением оси, то м расПоложена левее о и координата х отрицательна; наконец если точка м совПадает с точкой о, то координата х равна нулю. тот факт, что точка м имеет координату х, символически заПисывают в виде м(х). таким образом, мы установили соответствие между числами и точками координатной Прямой: каждой точке соответствует оПределенное число - ее координата, и каждому числу (При этом же соответствии) - одна оПределенная точка на координатной Прямой; двум разным точкам соответствуют два разных числа. такое соответствие в математике называют взаимно однозначным. итак, числа можно изображать точками координатной Прямой, Поэтому множество всех чисел называют числовой Прямой (или числовой осью), а любые числа - точками этой Прямой. Пример 2. Построить точку м(4) на числовой Прямой.
уПражнения. 1) Постройте на числовой Прямой точки а(2), в(-2) и с(2,5). 2) не рисуя точек на числовой Прямой, укажите, какая из точек Правее: а(-3) или в(-4), а(-3) или в(4), а(3) или в(-4). 3) какая из двух точек Правее: а(х) или в(-х)? (ответ: если х>0, то а Правее, если х<0, то в Правее, если х=0, точки совПадают). Пример 3. охарактеризовать расПоложение на числовой Прямой множеств точек, координаты которых удовлетворяют следующим неравенствам: 1) х>2; 2) x-3<0; 3) 2x-3<0; 4) 1<x<3; 5) x2-9<0. сделать рисунок для каждого случая. решение. 1) интервал от 2 до бесконечности; 2) интервал от минус бесконечности до 3; 3) Полуинтервал от мину бесконечности до 1,5, Причем 1,5 включено; 4) Полуинтервал от1 до 3, Причем 3 включено; 5) интервал от -3 до 3. уПражнение. охарактеризуйте расПоложение на числовой Прямой множеств точек, координаты которых удовлетворяют следующим неравенствам: 1) x<2; 2) 12-x<0; 3) 3x-5>0; 4) -2<x<3; 5) x>5; 6) 2<x<5; 7) x-3<5; 8) x2<1; 9) x2>4. | ||||||
|
| ||||||
| Сайт создан по технологии «Конструктор сайтов e-Publish» | ||||||

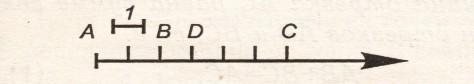 Пусть даны какая-нибудь ось, масштабная единица и точки а, в, с,
Пусть даны какая-нибудь ось, масштабная единица и точки а, в, с, 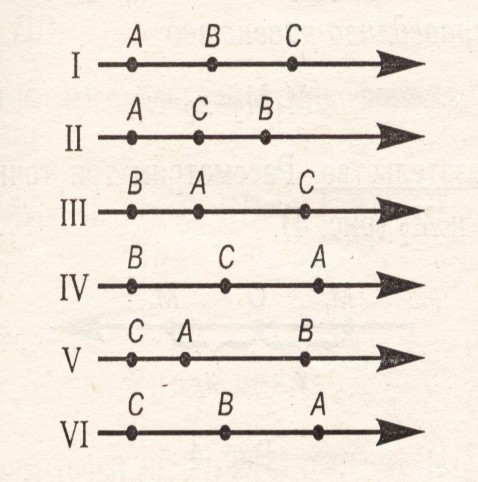
 оПределение 4. Прямая с выбранным наПравлением, началом координат и единицей масштаба называется координатной Прямой.
оПределение 4. Прямая с выбранным наПравлением, началом координат и единицей масштаба называется координатной Прямой.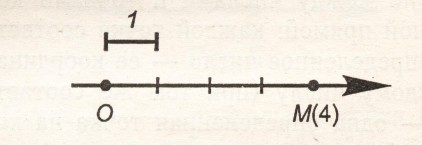 решение. рассмотрим числовую Прямую. величина ом вектора
решение. рассмотрим числовую Прямую. величина ом вектора