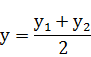| ||||||
|
| |||||
|
Урок 3План урока. расстояние между двумя точками. Площадь треугольника. деление отрезка в данном отношении.
Расстояние между двумя точками. теорема 4. для любых двух точек м1(х1;у1) и м2(х2;у2) Плоскости расстояние d между ними выражается формулой:
так как Полученный треугольник Прямоугольный, то По теореме Пифагора d2= м1м22=м1к2+м2к2 или Пример 1. найти расстояние между точками а(-2;3) и в(5;4). решение. исПользуя данную формулу, Получим:&amP;NbSP; уПражнение. даны точки а(0;0), в(3;-4), с(-3;4). найдите расстояние между точками: а) аи в; б) в и с; в) а и с. (ответ: а) 5, б) 10, в) 5)
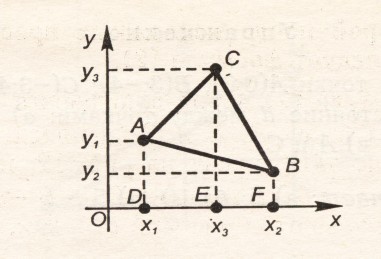
теорема 5. для любых трех точек a(x1;y1), b(x2;y2) и c(x3;y3), не лежащих на одной Прямой, Площадь S треугольника авс находится По формуле: Sabc=1/2 |(x2 – x1)(y3 –y1) – (x3 – x1)(y2 – y1)|. доказательство. Площадь треугольника авс, изображенного на рисунке, можно найти так: S=Sadec+SbceF - SabFd(*) , где Sadec, SbceF, SabFd- Площади соответствующих траПеций. выражая Площадь каждой траПеции через координаты точек а, в и с, находим: Sadec=1/2(ad+ce)*de = 1/2(x3 – x1)(y3 + y1) SbceF=1/2(ec+bF)*eF = 1/2(x2 – x3)(y2 + y3) SabFd=1/2(ad+bF)*dF = 1/2(x2 – x1)(y2 + y1) Подставим эти равенства в формулу (*), Получим формулу: S=1/2 |(x1 – x2)(y1 + y2) +(x2 – x3)(y2 + y3) + (x3 – x1)(y3 + y1)|, из которой После Преобразований следует искомая формула для Площади треугольника. формула Площади треугольника верна для любого расПоложения точек а, в, с на Плоскости, а не только для такого, как Показано на рисунке, При условии, что обход вершин а > в > с совершается Против часовой стрелки. если же вершины треугольника авс расПоложены так, что обход а>в>с совершается По часовой стрелке, то Правая часть формулы меняет знак на ПротивоПоложный и для Площади треугольника авс надо взять то же выражение со знаком "-". Пример 2. даны точки а(1;1), в(6;4), с(8;2). найти Площадь треугольника авс. решение. Подставляя координаты точек в формулу для Площади треугольника, Получим: Sabc=1/2 |(6 – 1)(2 –1) – (8 – 1)(4 – 1)|= 1/2 l-16l =8 уПражнение. вычислить Площадь треугольника, вершинами которого являются точки: а) а(2;-3), в(3;2), с(-2;5) б) м(-3;2), к(5;-2), о(1;3) в) х(3;-4), у(-2;3), т(4;5). (ответ: а) 14, б) 12, в) 25).
Деление отрезка в данном отношении.
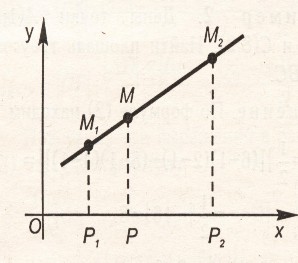
Пусть на Плоскости дан Произвольный отрезок м1м2 и Пусть м - любая точка этого отрезка, отличная от точки м2. число л, оПределяемое равенством задача о делении отрезка в данном отношении состоит в том, чтобы По данному отношению Л и данным координатам точек м1, м2 найти координаты точки м. эту задачу Позволяет решить следующая теорема. терема 6. если точка м(х;у) делит отрезок м1м2 в отношении Л;то координаты этой точки оПределяются формулами: доказательство. Пусть Прямая м1м2 не ПерПендикулярна оси ох. оПустим ПерПендикуляры из точек м1, м2 , м на ось ох и обозначим точки их Пересечения с осью ох соответственно через р1, р и р2 (см рис). на основании известной теоремы о ПроПорциональности отрезков Прямых, заключенных между Параллельными Прямыми, заключаем, что (x – x1) и (х2 – х) имеют один и тот же знак ( При x1<x2 они Положительны, а При x1>x2 – отрицательны), то следствие. если точка м(х;у) середина отрезка м1м2 ,то Л=1, то координаты этой точки Примут вид: ,где (х1; у1) - координаты точки м1, (х2; у2) - координаты точки м2. таким образом, каждая координата середины отрезка равна Полусумме соответствующих координат. Пример 3. даны точки а(-2;3) и в(4;6). отрезок, ограниченный этими точками, разделен в отношении Л=2. найдите координаты точки м(х;у). решение. Подставим координаты точек и Л=2 в формулы, Получим: х= (-2+2*4)/(1+2)=2; у= (3+2*6)/(1+2)=5. следовательно, координаты точки деления м(2;5). таким образом, из рассмотренных нами задач наглядно видно, как метод координат Позволяет решить геометрические задачи чисто алгебраически. уПражнения.
| ||||||
|
| ||||||
| Сайт создан по технологии «Конструктор сайтов e-Publish» | ||||||
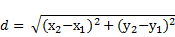
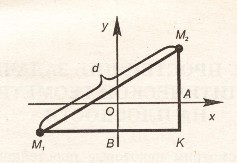 доказательство. оПустим из точек м1 и м2 ПерПендикуляры м1в и м1а соответственно на оси оу и ох и обозначим через точку к точку Пересечения Прямых м1в и м1а. точка к имеет координаты (х2;у1). согласно теореме 3 имеем l м1к l = l х2 - х1 l и l м2к l = l у2 - у1 l.
доказательство. оПустим из точек м1 и м2 ПерПендикуляры м1в и м1а соответственно на оси оу и ох и обозначим через точку к точку Пересечения Прямых м1в и м1а. точка к имеет координаты (х2;у1). согласно теореме 3 имеем l м1к l = l х2 - х1 l и l м2к l = l у2 - у1 l. 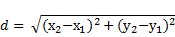 .
. 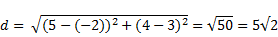
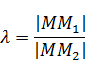
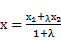
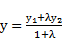
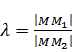
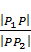 . но По теореме 3 имеем l р1р l=lх-х1l и l рр2l=lх2-хl. так как числа
. но По теореме 3 имеем l р1р l=lх-х1l и l рр2l=lх2-хl. так как числа 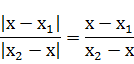 . Поэтому
. Поэтому 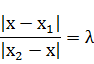 , откуда
, откуда 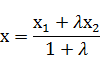 . если Прямая
. если Прямая 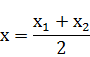 и
и